度量空间集聚的DO指数计算工具
今天推出的是DO指数计算工具。
DO 指数方法由Duranton and Overman(2005)提出,用于对产业空间集聚程度进行度量。 DO 指数的计算分为三步:
(1)计算核密度函数。假定行业\(I\)中存在\(n\) 家企业,运用每家企业的经纬度数据,可以计算出\(n( n- 1) /2\)个两两企业对彼此的空间距离,它与实际交通距离存在一定偏差,但对估计结果影响不大,Duranton and Overman(2005)曾详细阐述了这一问题。计算该行业两两企业彼此距离的核密度函数\(\hat{K}(d)\)的公式如下: \[ \hat{K}(d)=\frac{1}{n(n-1)h}\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}f(\frac{d-d_{i,j}}{h}) \] 其中,\(d\) 表示两两企业彼此的空间距离,\(d_{i,j}\)表示企业\(i\) 与企业\(j\) 之间距离值,\(f\)为高斯核密度函数,h 表示窗宽。
因为企业规模的大小会明显地影响企业的分布模式特征,所以本文采用企业就业人数作为规模的权重进入核密度函数,加入权重后公式如下:
\[\hat{K}^{EMP}(d)=\frac{1}{h\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}(e_{i}+e_{j})}\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}(e_{i}+e_{j})f(\frac{d-d_{i,j}}{h})\]
其中,\(e_i\)和\(e_j\)分别表示企业\(i\)与企业\(j\)的就业人数。Duranton and Overman(2005)最初使用\(e_ie_j\)项加权,但 Behrens and Bougna(2015)认为这样的设置会增加权重的极端差异,将其改为了\(e_i+e_j\)项加权,这里采用了该设置方法。
(2)反事实实验。为了识别行业\(I\)的空间分布模式,在计算该行业两两企业彼此距离的核密度函数后,再将其与无约束条件下企业随机分布假定的核密度函数进行比较。然而因为自然地理环境以及土地利用政策的局限,很多地区无法建造工业企业,因此,要利用目前约束条件下企业随机分布的核密度函数。本文构建以下反事实.将考察区域所有企业的位置信息表示为总集 S,从中随机地抽取 \(n\) 家企业位置数据代替行业 I 的企业进行空间分布的模拟 ,运用这 \(n\) 个模拟的经纬度数据, 由公式(10)计算出一次反事实的核密度函数。本文对每个行业重复反事实实验 1000 次。
(3)构造置信区间。根据固定距离\(d\),本文将获得的行业\(I\)的 1000 次反事实的核密度按升序进行排序,并选择 5%与 95%作为置信区间的下限\(\underline{K}_{I}(d)\)与上限\(\overline{K}_{I}(d)\),伴随着距离\(d\)的增加可得到置信带,该置信带一般被称为局部置信区间。对固定距离\(d\),当$ ( d) \(>\)I(d)\(时,该行业可认定为在某个距离点上以 95\)\(的置信水平呈现集聚状态;而当\)(d){<}_{}(d)$时,可认定为在某个距离点上以 95% 的置信水平呈现分散状态;其他情况为行业呈现随机分布特征。用 \(\varphi_I(d)\) 、\(\theta_I(d)\)分别代表局部集聚指数和分散指数:
工具界面如下:

可以根据需要,自行指定距离范围和迭代次数。
结果会生成一个包含K值和95%以及99%置信区间详细数值的excel结果文件,以及两张ggplot2风格的绘图,如下:
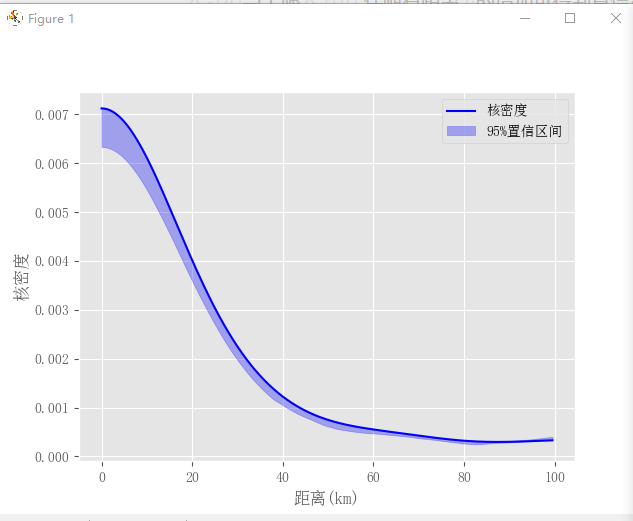
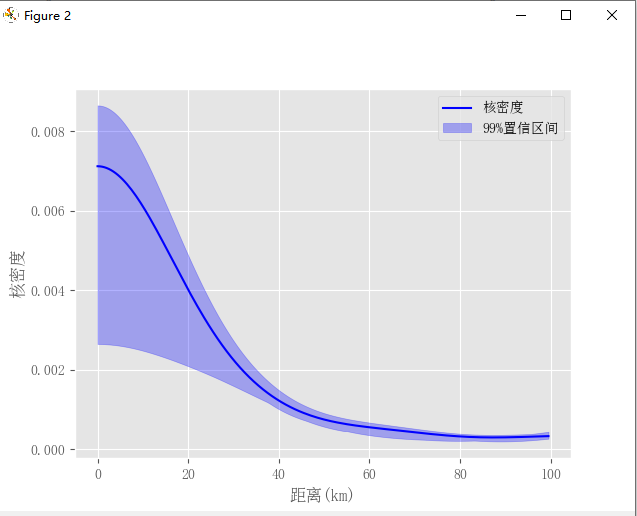
使用起来十分方便,需要的话,可以直接联系微信canglang12002
参考文献:《开发区政策影响中国产业空间集聚吗》孟美侠,曹希广,张学良
往期推文: 网络SBM模型(NSBM)复现
基于参数化的方向性距离函数(DDF)估算污染物影子价格的工具


