存在共享投入的两阶段博弈交叉DEA模型
今天推出的是存在共享投入的两阶段博弈交叉DEA模型。
网络 DEA 博弈交叉效率模型不仅适用于基本两阶段网络结构,还适用于多种网络结构,本文进一步将模型拓展为存在共享投入的两阶段DEA 博弈交叉效率模型。 存在共享投入的两阶段网络结构中,假设有 n 个 DMU;在第一阶段,\(DMU_j(j=1,2,...,n)\)用 m 种共享比例分别为\(\alpha_{ij}(i=1,2,...,m)\)的外源投入\(x_ij(i=1,2,...,m)\)产生 q 种产出\(z_pj(p=1,2,...,q);\) 在第二阶段,\(DMU_{j}(j=1,2,...,n)\)用 m 种共享比例分别为的外源投入\[(1-\alpha_{i_{i}})\],\(x_{ij}(i=1,2,....,m)\)和第一阶段的 q 种产出\(z_{pj}(p=1,2,...,q)\)产生 S 种产出\(y_{rj}(r=1,2,....,s)\),这 S 种产出离开系统。其中,共享比例\(\alpha_{i_i}(i=1,2,...,m)\)是未知参数,管理者可根据现实情况设置共享比例的下界\(L_{ij}\) 和上界\(U_{ij}\)。
其模型最终的规划式如下: \[ \begin{array}{ll}\max & E_{d k}^{(g)}=\sum_{r=1}^{s} \mu_{r k}^{d(g)} y_{r k}+\sum_{p=1}^{q} \omega_{p k}^{d(g)} z_{p k} \\\text { s.t. } & \sum_{i=1}^{m} v_{i k}^{d(g)} x_{i k}+\sum_{p=1}^{q} \omega_{p k}^{d(g)} z_{p k}=1, \\& \sum_{p=1}^{q} \omega_{p k}^{d(g)} z_{p j}-\sum_{i=1}^{m} \beta_{i j}^{d(g)} x_{i j} \leq 0, j=1, \ldots, n, \\& \sum_{r=1}^{s} \mu_{r k}^{d(g)} y_{r j}-\sum_{i=1}^{m} \nu_{i k}^{d(g)} x_{i j}+\sum_{i=1}^{m} \beta_{i j}^{d(g)} x_{i j}-\sum_{p=1}^{q} \omega_{p k}^{d(g)} z_{p j} \leq 0, j=1, \ldots, n \\& E_{d}^{(g-1)} \sum_{i=1}^{m} v_{i k}^{d(g)} x_{i d}+\left(E_{d}^{(g-1)}-1\right) \sum_{p=1}^{q} \omega_{p k}^{d(g)} z_{p d}-\sum_{r=1}^{s} \mu_{r k}^{d(g)} y_{r d} \leq 0, \\& L_{i j} \nu_{i k}^{d(g)} \leq \beta_{i j}^{d(g)} \leq U_{i j} \nu_{i k}^{d(g)}, i=1, \ldots, m ; j=1, \ldots, n, \\& v_{i k}^{d(g)}, \omega_{p k}^{d(g)}, \mu_{r k}^{d(g)} \geq 0, \quad i=1, \ldots, m ; p=1, \ldots, q ; r=1, \ldots, s .\end{array} \] 两阶段博弈DEA模型,由于需要大量计算,如有N个DMU,那么需要进行G*N^2次的线性规划,为了加快运行速度,在计算式采用文献中提供的新的算法设计。其具体思路如下:
第一步:将 g=1 时每个 DMU 博弈前的平均整体交叉效率设置为 0.001,即令 g=1 时(式 3.7)中\(E_d^{( \mathbf{0} ) }= 0. 001\) \(( d= 1, 2, . . . , n)\),并求解(式 3.7)至(式 3.11),计算\(DMU_k(k=1,2,...,n)\)第 1 次博弈后的平均整体交叉效率\(E_k^{(\mathrm{l})}\)、平均第一阶段交叉效率\(E_k^{\mathrm{l}(\mathrm{l})}\)以及平均第二阶段交叉效率\(E_k^{2(\mathrm{l})};\) 第二步:当 g=2 时,求解(式 3.7)至(式 3.11),计算\(DMU_k(k=1,2,...,n)\)第 g 次博弈后的平均整体交叉效率\(E_k^{(2)}\)、平均第一阶段交叉效率\(E_k^{1(2)}\)以及平均第二阶段交叉效率\(E_k^{2( 2) }\) ;
第三步:当 g=3 时,令\(E_k^{(3)}=\frac{E_k^{(1)}+E_k^{(2)}}2(k=1,2,...,n)\)、\(E_k^{1(3)}=\frac{E_k^{1(1)}+E_k^{1(2)}}2\)
\((k=1,2,...,n)\)和\(E_{k}^{2(3)}=\frac{E_{k}^{2(1)}+E_{k}^{2(2)}}{2}\left(k=1,2,...,n\right);\)
第四步:当\(g\geq4\)时,求解(式 3.7)至(式 3.11),计算 \(DMU_k(k=1,2,...,n)\)第 g 次博弈后的平均整体交叉效率\(E_k^{(\mathrm{g})}\)、平均第一阶段交叉效率\(E_k^{1(\mathrm{s})}\)以及平均第二阶段交叉效率\(E_k^{2(g)};\) 第五步:判断第四步每个\(DMU_k(k=1,2,...,n)\)的计算结果是否满足\(\left|E_k^{(\mathrm{g}+1)}-E_k^{(\mathrm{g})}\right|\leq\varepsilon,\left|E_k^{\mathrm{l}(\mathrm{g}+1)}-E_k^{\mathrm{l}(\mathrm{g})}\right|\leq\varepsilon,\left|E_k^{2(\mathrm{g}+1)}-E_k^{2(\mathrm{g})}\right|\leq\varepsilon(k=1,2,...,n)\),若存在 DMU 不满足此三个不等式中的任一不等式则重复第四步,直到所有 DMU 都满足上述不等式。
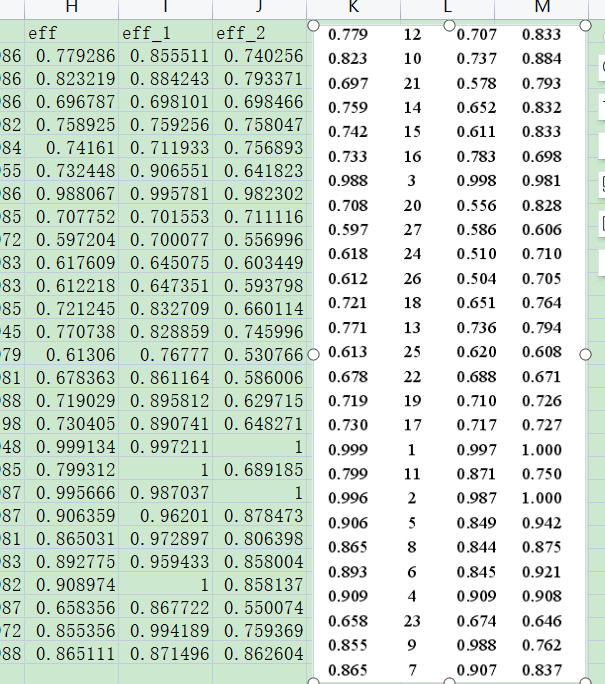
关于该模型,使用matlab和julia分别完成了模型建模,均能得到和论文相同的结果(指总效率,分阶段效率有差异,但是排名与论文中的结果近似。这是由于最优解不唯一造成的。)
对比如下:
参考文献:《网络DEA中的交叉效率及其应用研究》
有需要的同学可以联系微信: canglang12002


