基尼系数双维度分解工具
基尼系数双维度分解计算工具
今天推出的是一个基尼系数双维度分解工具,之前的基尼系数分解,要么是基不同的子群,或者基于不同的分项,但是有时候我们需要同时基于分组和分项来研究,如GDP,既需要根据区域分组研究区域差异,也需要揭示总体差异的产业来源,这时候常用的泰尔指数、Dagum基尼系数分解就不再适用了。
这个基尼系数双维度分解是由Mussard在2004年提出,其主要理论如下:
给定一个样本总体\(P\),其规模为\(n\),均值为\(\mu\),该总体划分为\(k\) 个子群,每个子群可以表示为\(P_i(\forall j,h=1\), 2,...,k)。每一个子群的均值和规模分别表示为\(\mu_j\)和\(n_j\)。基尼系数可以用下面的公式来计算,其中,\(s_{p,i},s_{p,r}\)分别表示样本总体\(P\)中的个体\(i\)、个体\(r\) 的指标\(\langle i=1,2,\cdots,n\rangle\)。
\[ G=\frac{\hat{\sum}_{i=1}\hat{\sum}_{r=1}|x_{p,i}-x_{p,r}|}{2\mu n^{2}} \]
总体指标被分成 \(q\) 个来源 \(x^m(m=1,2,\cdots,q)\) 。在样本总体 \(P\) 中,每个个体的指标可以表示为:
\[ x_{_{P,i}}=\sum_{n=1}^{q}x_{P,i}^{m} \]
由于
\[ \mid x_{p,i}-x_{p,r}\mid=x_{p,i}+x_{p,r}-2\mathrm{min}\{x_{p,i},x_{p,r}\} \]
因此,总体\(P\) 的基尼系数可以表示为:
\[ G=\frac{\sum_{i=1}^{n}\sum_{i=1}^{n}\left(x_{p,i}+x_{p,r}-2\min\{x_{p,i},x_{p,r}\}\:\right)}{2\mu n^2} \]
下面,根据总体指标来源对 2min\(\{x_{p,i},x_{p,r}\}\) 进行分解:
\[ \sum_{m=1}^{q} 2 x_{P, i r}^{* m}=2 \min \left\{x_{P, i}, x_{P, r}\right\} \]
例如,令\(2x_{p,i}=2\min\{x_{p,i},x_{p,r}\}\),如果\(x_{p,i}=x_{p,i}^1+x_{p,i}^2\),那么
\[ \sum_{m=1}^{q}2x_{P,ir}^{^*m}=2*(x_{P,i}^{^1}+x_{P,i}^{^2}) \]
因此,基尼系数可以按照分项指标进行如下测度:
\[ G=\sum_{n=1}^{q}\left(\frac{\sum_{i=1}^{n}\sum_{i=1}^{n}(x_{P,i}^{m}+x_{P,r}^{m}-2x_{P,ir}^{m})}{2\mu n^{2}}\right) \]
上式表明基尼系数被分解成 q 个部分,每个部分就是该指标各分项指标对于总体差异的贡献。根据 Dagum的基尼系数分解方法,基尼系数可以按照子群进行分解:
\[ G=\frac{\sum_{j=1}^{k}\left(\sum_{i=1}^{n j}\left|x_{j, i}-x_{j, r}\right|\right)}{2 \mu n^{2}}+\frac{2 \sum_{j=2}^{k} \sum_{h=1}^{j-1}\left(\sum_{i=1}^{n j} \sum_{r=1}^{n h}\left|x_{j, i}-x_{h, r}\right|\right)}{2 \mu n^{2}} \]
其中,\(x_{j,r}\)表示第\(j\) 个子群中第 r 个个体的指标。按照 Dagum,基尼系数分解为两个部分:
\[ G=G_{_{w}}+G_{_{gb}} \]
其中,\(G_{_w}\) 是区域内差异;\(G_{gb}\) 是区域间差异。基尼系数的双维分解可以按照如下公式进行:
\[ G=\sum_{m=1}^{q}\left\{\frac{\sum_{j=1}^{k}\left[\:\sum_{i=1}^{nj}\:\sum_{r=1}^{nj}\:(\:x_{j,i}^{m}+x_{j,r}^{m}-2x_{j,ir}^{s\:m})\:\right]}{2\mu n^{2}}\right\}+\sum_{m=1}^{q}\left\{\frac{2\sum_{j=2}^{k}\:\sum_{k=1}^{j-1}\left[\:\sum_{i=1}^{nj}\:\sum_{r=1}^{nk}\:(\:x_{j,i}^{m}+x_{k,r}^{m}-2x_{jk,ir}^{s\:m})\:\right]}{2\mu n^{2}}\right\} \]
该模型计算过程比较复杂,我们开发出相关工具,可以直接计算基尼系数的双维度分解,结果如下:
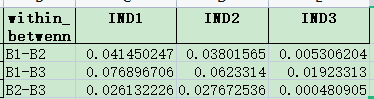

分别是组内GINI和组间GINI,其和应等于总体GINI。
我们这个工具特点之一,就是可以在结果中指明对应分组的名称,而非用数字代替,简洁明了。
有需要可以联系微信:canglang12002


